Since the introduction of Swift, the iOS community has been buzzing with the words functional programming.
That’s because many features of Swift were inspired by the ones you find in functional programming languages.
These features make some tasks easier. One example is easily configurable callbacks for network requests.
While Swift is not a functional language, we can draw many lessons from functional programming to write better Swift code in our iOS apps.

FREE GUIDE - SwiftUI App Architecture: Design Patterns and Best Practices
MVC, MVVM, and MV in SwiftUI, plus practical lessons on code encapsulation and data flow.
DOWNLOAD THE FREE GUIDEContents
Section 1:
Swift as a multi-paradigm language

Swift is not a functional language, but a multi-paradigm one. While it’s possible to write functional code in Swift, you should not try to force it where it does not make sense.
Swift is not a functional language, and the iOS SDK is object-oriented
Before we explore functional programming ideas in Swift, it’s worth mentioning that Swift is not a functional language, and it is not meant to be one.
Swift is different from purely functional languages like Haskell, and the object-oriented paradigm you are used to is quite different from the functional model.
For example, purely functional languages do not have loop constructs like for or while (I will show you later how it is still possible to write programs without them). Moreover, in those languages, you need to understand concepts like functors and monads.
That’s not the case in Swift.
Some functional languages like Lisp are multi-paradigm because they also allow object-oriented programming. But they remain functional at heart, and some Lisp dialects like Clojure eschew the traditional object-oriented approach.
In iOS though, we have to write programs mostly in the object-oriented paradigm.
Some developers try to cram functional programming concepts into every aspect of iOS development, getting to the extreme of making view controllers functional.
I find that to be just counterproductive.
Your code will be unfamiliar to most other iOS developers. More to the point, you will soon bump into the limitation of the platform. View controllers are classes with a particular lifecycle.
There is no way to escape that.
The pillar of functional programming: transforming an input into an output
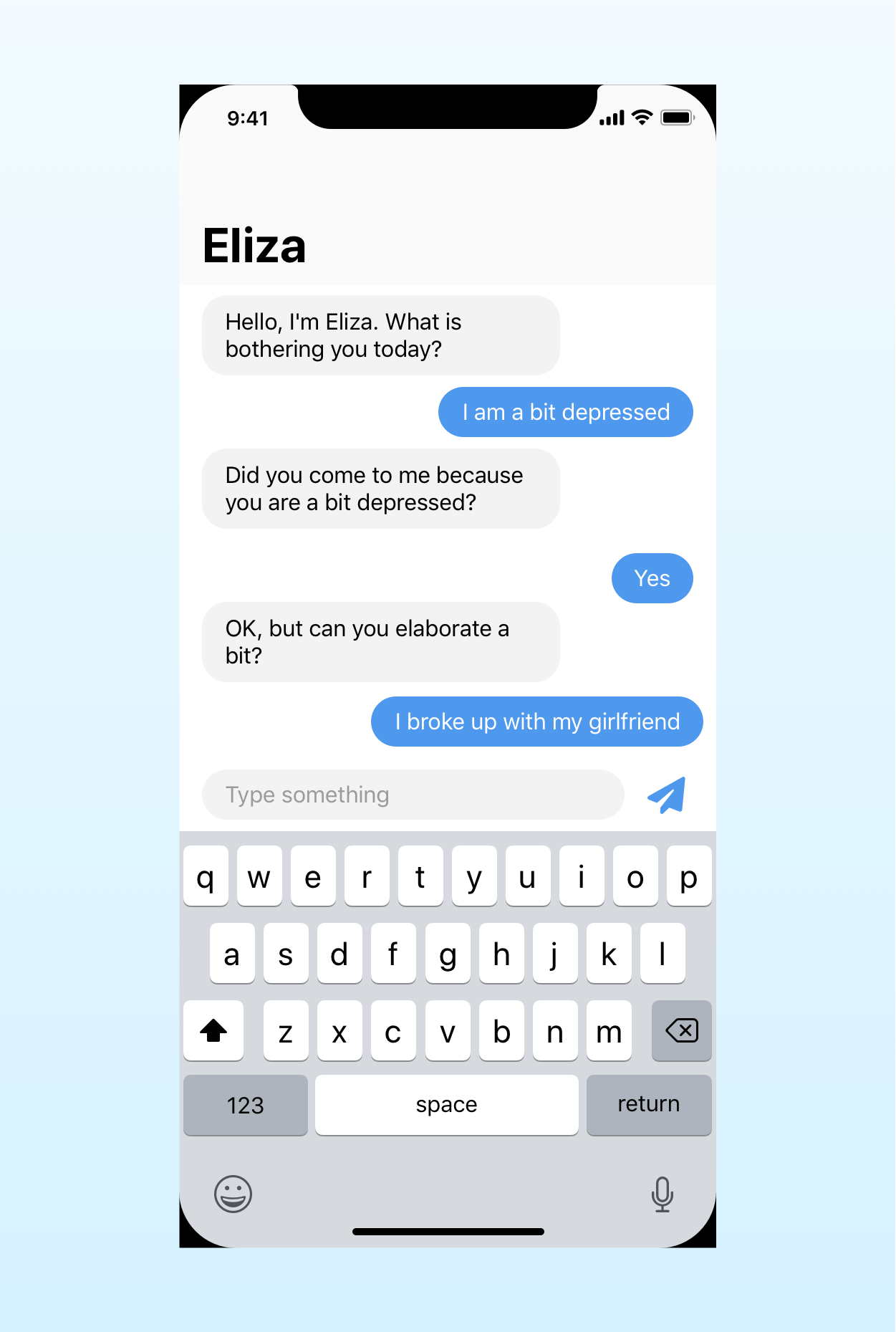
In this article, I will build a small Eliza chatbot to show you how to use functional programming concepts in a real app. You can find the full project on GitHub.
Eliza is a natural language processing program based on Rogerian psychotherapy.
While that might sound complex, all Eliza does is turn everything you write into a question. For example, if you state “I feel sad” it will ask you something like “Do you often feel sad?”
Eliza does not use any fancy AI algorithm like deep learning or neural networks. It merely consults a list of predefined answers.
At its core, Eliza is built around the pillar of functional programming: it transforms an input into an output. This makes it a widespread functional programming exercise, of which you can find many implementations online.
In fact, the implementation that I will show you in this article comes code that I wrote ten years ago to learn functional programming.
Writing an app’s code top-down instead of bottom-up
We will implement this app top-down. We will start from the user interface and then proceed through the view controller level, all the way down to the algorithm details.
I usually follow a bottom-up approach in many of my articles. That makes it easier for me to decompose a problem and explain the code step-by-step.
But writing code top-down is also a sound, and sometimes preferable, approach especially if you adhere to the dependency inversion principle.
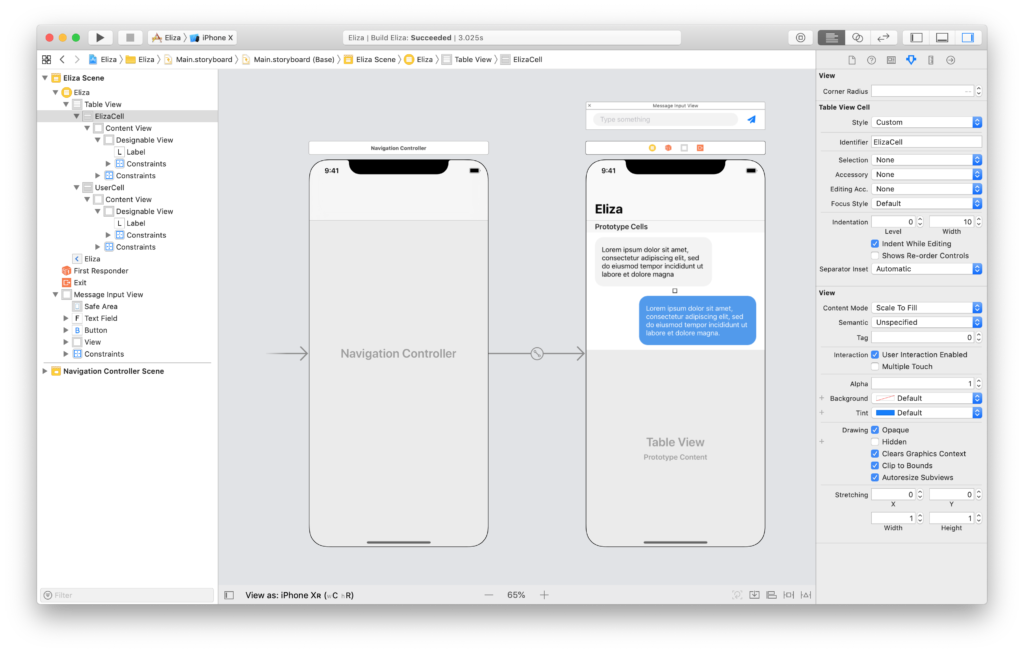
So, we will start from the app’s storyboard. This contains only a simple table view controller that will display a conversation with Eliza.
Not all the UI fits in the storyboard. Our view controller needs to set an input view where the user can type a message. While the view can be laid out in the storyboard scene, we also need some setup code.
class ChatViewController: UITableViewController {
@IBOutlet var messageInputView: UIView!
@IBOutlet var textField: UITextField!
override var inputAccessoryView: UIView? {
return messageInputView
}
override func viewDidAppear(_ animated: Bool) {
super.viewDidAppear(animated)
textField.becomeFirstResponder()
}
override var canBecomeFirstResponder: Bool {
return true
}
}View controllers and other UIKit code cannot be functional
All our view controller needs to do is populate its table view.
Typically, I would create a separate data source class for a dynamic UITableView, but to keep this example simple, I will use the view controller.
ChatViewController: UITableViewController {
@IBOutlet var messageInputView: UIView!
@IBOutlet var textField: UITextField!
var messages: [String] = ["Hello, I'm Eliza. What is bothering you today?"]
override var inputAccessoryView: UIView? {
return messageInputView
}
override func viewDidAppear(_ animated: Bool) {
super.viewDidAppear(animated)
textField.becomeFirstResponder()
}
override var canBecomeFirstResponder: Bool {
return true
}
override func tableView(_ tableView: UITableView, numberOfRowsInSection section: Int) -> Int {
return messages.count
}
override func tableView(_ tableView: UITableView, cellForRowAt indexPath: IndexPath) -> UITableViewCell {
let row = indexPath.row
let identifier = row.isMultiple(of: 2) ? "ElizaCell" : "UserCell"
let cell = tableView.dequeueReusableCell(withIdentifier: identifier, for: indexPath) as! MessageCell
cell.message = messages[row]
return cell
}
}
class MessageCell: UITableViewCell {
@IBOutlet weak var label: UILabel!
var message: String? {
didSet { label.text = message }
}
}Here, we keep the chat messages in a simple array of strings. Then, to use the correct color for a bubble, we dequeue a cell for Eliza for rows with an even index, and a cell for the user for odd rows. (Don’t forget to set the cell identifiers in the storyboard.)
Pushing new messages into the chat is simple. All we have to do is:
- append the new message at the end of the
messagesarray; - insert a new row at the bottom of the table view; and
- scroll the table view so that the last message is always visible.
private extension ChatViewController {
func push(_ message: String) {
messages.append(message)
let newMessageIndexPath = IndexPath(row: messages.count - 1, section: 0)
tableView.insertRows(at: [newMessageIndexPath], with: .fade)
tableView.scrollToRow(at: newMessageIndexPath, at: .bottom, animated: true)
}
}At a high level, all our Eliza chatbot needs to do is reply to a message.
struct Eliza {
func reply(to message: String) -> String {
return ""
}
}Finally, when the user sends a message, we push it into the chat, and then push Eliza’s reply.
class ChatViewController: UITableViewController {
@IBOutlet var messageInputView: UIView!
@IBOutlet var textField: UITextField!
var messages: [String] = ["Hello, I'm Eliza. What is bothering you today?"]
override var inputAccessoryView: UIView? {
return messageInputView
}
override func viewDidAppear(_ animated: Bool) {
super.viewDidAppear(animated)
textField.becomeFirstResponder()
}
override var canBecomeFirstResponder: Bool {
return true
}
@IBAction func send(_ sender: Any) {
guard let message = textField.text, !message.isEmpty else {
return
}
push(message)
textField.text = nil
push(Eliza().reply(to: message))
}
override func tableView(_ tableView: UITableView, numberOfRowsInSection section: Int) -> Int {
return messages.count
}
override func tableView(_ tableView: UITableView, cellForRowAt indexPath: IndexPath) -> UITableViewCell {
let row = indexPath.row
let identifier = row.isMultiple(of: 2) ? "ElizaCell" : "UserCell"
let cell = tableView.dequeueReusableCell(withIdentifier: identifier, for: indexPath) as! MessageCell
cell.message = messages[row]
return cell
}
}Since we are writing code top-down, at the moment the reply(to:) method of the Eliza struct just returns an empty string.
This allows us to finish our ChatViewController implementation before focusing on the Eliza algorithm. I will follow this approach throughout this article.
Section 2:
The functional programming paradigm in swift

Functional programming is not simply a style of writing code. It’s a different paradigm which makes you think about code in a new way.
The imperative paradigm focuses on describing how a program works
Before we start writing functional code, we first need to answer a fundamental question.
What makes functional programming so different?
All the name implies is that it uses functions. But we already put all our Swift code into functions. So, isn’t that functional programming as well?
Obviously, it isn’t, or I would not be writing this article. The difference is in the paradigm. The programming paradigm you (and most developers) are used to is called imperative.
In imperative programming, we write a series of instructions that change the internal state of a program. What we focus on is describing how a program operates.
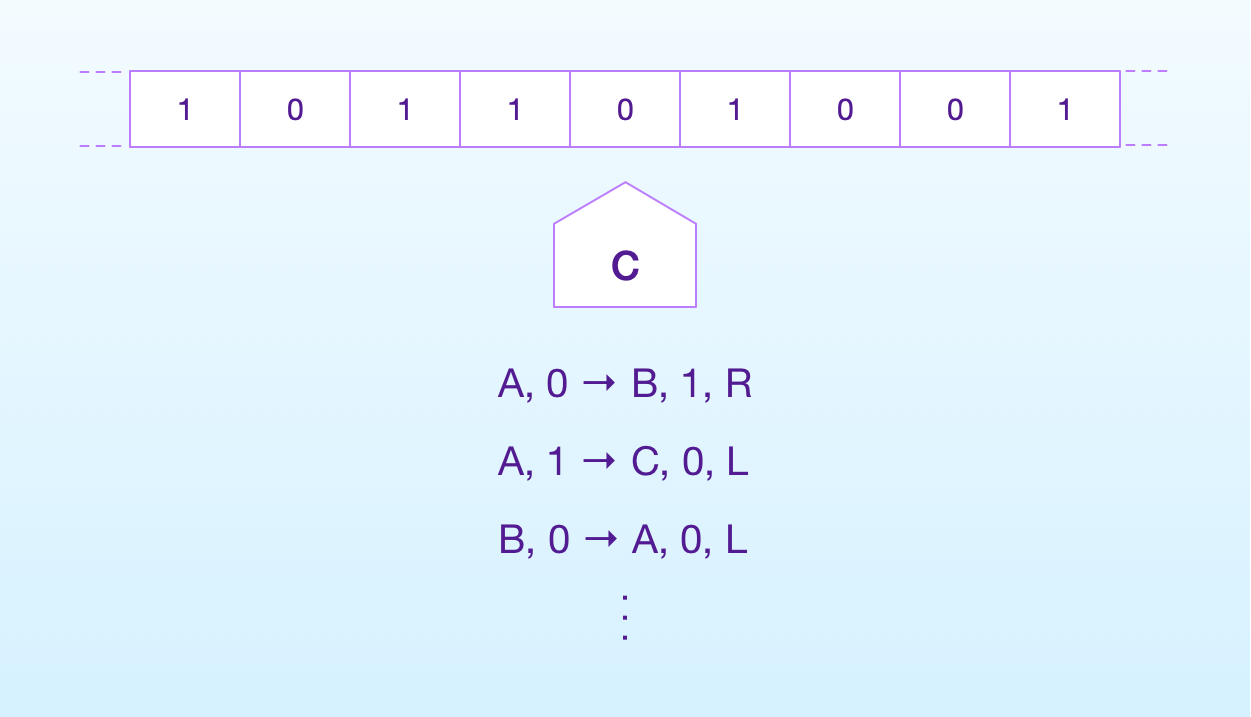
Imperative programming is based on a mathematical computational model called Turing machine.
In short, a Turing machine has:
- an internal state;
- an infinite memory tape;
- a head that can move left or right on the tape and read and write data; and
- a table of instructions describing how it works.
Each instruction reads the state of the machine and the data on the tape. As a result, the head can move and write new data on the tape, and the machine can change state.
It should not be hard for you to see the similarity between this model and the programs you write.
The code we wrote in the ChatViewController above is imperative. Each method is made of a series of instructions that change the internal state of the app.
Functional programming focuses on what a program does, not on how it works.
Turing machines are not the only mathematical model of computation.
There is another one called Lambda calculus, which was invented before Turing machines. Although to be fair, Turing machines are based on the Analytical Engine, which came one century earlier.
At first sight, lambda calculus looks weird.
We don’t need to care about how lambda calculus works, although it’s a fascinating topic (if you wonder why I know so much about it, I made a master thesis on it).
What we care about is that it is based on the mathematical idea of pure functions.
A pure function:
- Returns values that depend solely on its parameters. It does not access any global variables (like singletons, non-local variables (like the properties of a class or a structure) or any other input stream (files, device sensors, etc.).
- Does not produce any side effect. It returns only a value, without mutating any state outside of its scope.
The banal reply(to:) method we wrote in the Eliza structure is a pure function. We will find plenty of more examples in this article.
It turns out that Turing machines and Lambda calculus are equivalents. This means we can also base a programming paradigm on Lambda calculus, which allows us to do anything we can do in imperative programming.
That’s precisely what the creators of Lisp did, creating functional programming.
A functional program is not imperative, but declarative, which means that it focuses on what a program does and not on how it works.
The benefits of writing functional Swift code
At this point, a spontaneous question arises.
Why should we care?
After all, we can already write Swift programs using the imperative paradigm. Who cares about fancy academic languages very few developers use.
As it turns out, pure functions have some desirable properties.
- Pure functions always produce the same result for the same input. That makes them straightforward to test. To instead test code that produces side effects, we need test doubles and other sophisticated techniques.
- Pure functions are (sometimes) easier to read and understand. When reading a piece of code uses a pure function, you don’t need to worry about its internal implementation. You only care about the return value, because you are sure that it does not produce any side effect.
- Pure functions simplify concurrency. Since they do not access any shared resource, there is no risk of causing race conditions. You can safely call them from parallel threads, without relying on locks, or operation queues, avoiding the risk of deadlocks.
As I said above, Swift is not a functional language, so it’s impossible to make all the functions/methods in an iOS app pure. That is why the code of our ChatViewController is imperative.
But functional programming works when specifying the business logic of an app.
Writing declarative, functional Swift code by chaining functions
Now that we have seen the distinction between the imperative and functional paradigms, in theory, let’s look at it in practice.
This difference is not immediately noticeable, so we will approach it step-by-step throughout the rest of this article.
In imperative programming, we usually think about the discrete steps we need to go through to get to a result. To do so, we use assignments, branching statements, and for loops.
In functional programming, instead, we think about how to transform an input into output through a series of consecutive functions.
The Eliza algorithm creates a reply for a user message using a predefined table of patterns.
Since we will have to match a user message to one of those patterns, it’s useful to clean the user input, removing symbols and making all letters lowercase.
Here we can see the first example of declarative programming:
- Remove symbols from the user message.
- Make the result of the previous step lowercase.
- Transform the result of the previous step into a reply.
struct Eliza {
func reply(to message: String) -> String {
let message = message
.removingAllSymbols()
.lowercased()
return transform(message: message)
}
}
private extension Eliza {
func transform(message: String) -> String {
return message
}
}
extension String {
func removingAllSymbols() -> String {
return self
}
}This code is functional because it only uses pure functions that transform the output of a previous function.
Here you can see that in Swift we have two ways to write pure functions:
- The
transform(message:)function takes its input as a parameter. - The
removingAllSymbols()andlowercased()functions, instead, are methods of theStringtype. Their input is the value on which they are called. They are still technically pure functions because they only depend on their input and do not create side effects.
Section 3:
The core ideas of functional programming
Functional programming uses constructs that are different from the ones you find in imperative programming. Instead of relying on polymorphism and loops, functional programming uses higher-order functions for abstraction and the map, filter and reduce functions for iteration.
Abstracting code in functional programming using higher-order functions
In any program, we often need to reuse code to avoid repetitions. Functions are, of course, the primary way to reuse code.
As we reuse code, we make it more abstract, to accept the most extensive number of cases possible.
Functions alone, though, are not enough as an abstraction mechanism.
In Swift’s object-oriented or protocol-oriented programming, we make our code more abstract through polymorphism, by either:
- moving a method into a superclass or a protocol, so that all the subtypes can inherit it; or
- using superclasses, protocols, and generics as the types for the parameters of a function.
In purely functional languages, there are no classes or protocols. The only abstraction available is, you guessed it, the function.
We can still make our code more generic though, using higher-order functions.
A higher-order function is a function that either:
- takes a function as an argument, or
- returns a function.
Of course, both are possible at the same time.
Higher-order functions enable function composition, allowing you to combine two functions to create a new one. In Swift, there are plenty of higher-order functions you probably used already.
For example, the dataTask(with:completionHandler:) method of URLSession is a higher-order function. The completion handler is a function that gets called when the network transfer is finished.
In functional programming, there are three important higher-order functions: map, filter, and reduce.
The filter function remove elements from a sequence
Let’s start from the filter function, which is the easiest of the three.
In short, filter removes from a sequence all the elements that do not satisfy a predicate.
More in detail, in Swift the filter(_:) function of the Sequence protocol:
- takes a predicate that returns a boolean;
- returns an array containing the elements for which the predicate returns
true.
For example, we can use filter to get all the numbers in an array that are even, or bigger than another number.
let numbers = [1, 9, 7, 2, 5, 4, 6]
numbers.filter { $0 > 3 }
// returns [9, 7, 5, 4, 6]
numbers.filter { $0.isMultiple(of: 2) }
// returns [2, 4, 6]In our Eliza app, we can use filter to remove all the symbols from a message.
String {
func removingAllSymbols() -> String {
return self.filter { character in
return character
.unicodeScalars
.allSatisfy{ CharacterSet.symbols.contains($0) }
}
}
}A string in Swift can be seen as a sequence of characters, so that’s what the filter function operates on.
In Swift, there is no direct way to know if a character is a symbol. So, in the code above, the predicate is a sequence of functions that returns true when the Unicode scalars of a character are not in the CharacterSet for symbols.
The allSatisfy(_:) function is another higher-order function.
Here you can see the first, partial explanation of how it is possible to write programs without loops. Functions like filter(_:) iterate over a sequence and return another one, so we don’t need a loop.
I can already hear you object: “But wait, that’s just a trick! The loop is just hidden inside the filter function”.
That’s true. If we look at the implementation of filter in Swift, it contains a while loop:
@inlinable
public __consuming func filter(
_ isIncluded: (Element) throws -> Bool
) rethrows -> [Element] {
return try _filter(isIncluded)
}
@_transparent
public func _filter(
_ isIncluded: (Element) throws -> Bool
) rethrows -> [Element] {
var result = ContiguousArray<Element>()
var iterator = self.makeIterator()
while let element = iterator.next() {
if try isIncluded(element) {
result.append(element)
}
}
return Array(result)
}As I said, this is just a partial explanation. I will give you the full answer later.
The map function transforms a sequence into another one
The next in the set of “iterative” functions is the map function.
In short, map transforms all the elements in a sequence one by one and returns the results.
More in detail, in Swift the map(_:) function of the Sequence protocol:
- takes a transforming function;
- returns an array containing the results of applying the transforming function to each element of the sequence.
For example, we can use map(_:) to calculate the square of all the numbers in an array.
func square(x: Int) -> Int {
return x * x
}
let numbers = [1, 9, 7, 2, 5, 4, 6]
numbers.map(square)
//returns [1, 81, 49, 4, 25, 16, 36]When Eliza replies to a message, it has to change the person of pronouns and verbs in the first or second person.
For example, a sentence like “I can’t talk to my father” should become “What would it take for you to talk to your father?”. While the first part of the reply will come from a template, the second is derived from the user message, where my has been changed to your.
Let’s start writing a function that reflects a single word. We can do so by putting all the possible transformations in a dictionary since they are not that many.
struct Reflector {
}
private extension Reflector {
func reflect(word: String) -> String {
return StaticData.reflections[word] ?? word
}
}
struct StaticData {}
extension StaticData {
static var reflections: [String: String] {
return [
"am": "are",
"was": "were",
"i": "you",
"i'm": "you are",
"i'd": "you would",
"i've": "you have",
"i'll": "you will",
"my": "your",
"me": "you",
"are": "am",
"you're": "I am",
"you've": "I have",
"you'll": "I will",
"your": "my",
"yours": "mine",
"you": "me"
]
}
}To then reflect a full sentence, we can break it into words and then map the reflect(word:_) function over them. After that, we join the resulting array to get back a string.
struct Reflector {
func reflect(sentence: String) -> String {
return sentence
.components(separatedBy: .whitespaces)
.map (reflect(word:))
.joined(separator: " ")
}
}
private extension Reflector {
func reflect(word: String) -> String {
return StaticData.reflections[word] ?? word
}
}This works, but our functions are not pure anymore. The result reflect(word:_) does not depend only on the word parameter, but also on the reflection property of StaticData.
Since we are not using a purely functional language, we don’t have to make every function pure. But if you want, or need to, you can use a simple trick.
The dictionary of reflections is just another input of the reflect(word:_). We just have to make that explicit.
struct Reflector {
func reflect(sentence: String) -> String {
return sentence
.components(separatedBy: .whitespaces)
.map { reflect(word: $0, with: StaticData.reflections) }
.joined(separator: " ")
}
}
private extension Reflector {
func reflect(word: String, with reflections: [String: String]) -> String {
return reflections[word] ?? word
}
}The reflect(word:with:) function is now pure.
While reflect(sentence:_) is not, you can make it pure using the same trick. But at some point, somewhere, you will have a function that is not pure. That’s just the nature of iOS apps.
The reduce function combines the elements of a sequence
The last of the three iterative functions is the reduce function.
In short, reduce combines the elements of a sequence into a single value.
More in detail, in Swift the reduce(_:) function of the Sequence protocol:
- takes an initial value from which to start the combination;
- takes a function that combines two values into a third one;
- iterates over the elements of the sequence and combines the current element with the result of the previous combination.
Of the three iterative functions, reduce(_:) is the hardest to use, and the least common. But it’s still necessary from time to time.
For example, we can use reduce(_:) to sum or multiply all the numbers in an array, or to combine a list of booleans.
let numbers = [1, 9, 7, 2, 5, 4, 6]
numbers.reduce(0, +)
// returns 34
numbers.reduce(1, *)
// returns 15120
let booleans = [true, false, true, true, false]
booleans.reduce(true, { $0 && $1 })
// returns false
booleans.reduce(false, { $0 || $1 })
// returns trueAs you can see, the initial value depends on the way you combine the elements in the sequence. In a sum, we start at 0, which is the identity element for the addition operation. In a product, we start at 1.
For booleans, the && operator returns true only when all the values are true, so that’s our initial value. The || operator instead returns true when at least one of the values is true, so we start from false.
The initial value for the reduce(_:) function is not always straightforward.
For example, if you want to concatenate words, starting from an empty string only works when you don’t need spaces between words.
In the reflect(sentence:) function, we joined the reflected words in a sentence using the joined(separator:) function of Array. That is a convenience function that relies on reduce(_:), relieving us from the pain of picking the initial value.
If we didn’t have that function and we had to use reduce(_:) instead, this is how we would write reflect(sentence:):
struct Reflector {
func reflect(sentence: String) -> String {
let reflected = sentence
.components(separatedBy: .whitespaces)
.map { reflect(word: $0, with: StaticData.reflections) }
return reflected
.dropFirst()
.reduce("\(reflected[0])", { $0 + " " + $1 })
}
}To avoid placing a space at the beginning of the sentence, the initial value of reduce(_:) needs to be the first element of the sequence. This means that we need to call reduce(_:) only on the remaining elements of the sequence.
The functional Eliza algorithm
Now that we have laid some of the groundwork for our app let’s look at the Eliza algorithm in detail.
The Eliza chatbot is based on a set of predefined rules. Each rule provides a few canned answers that the chatbot can use to transform what the user says into a question.
Each rule has:
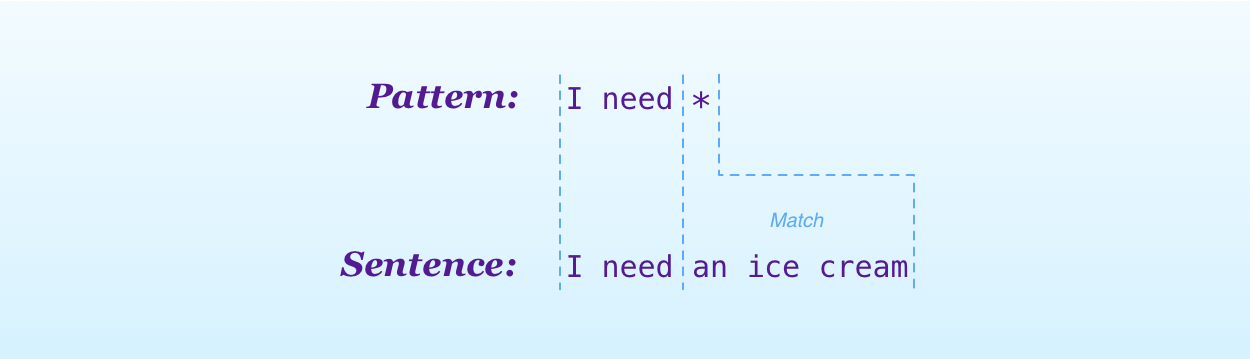
- a pattern to match a message. Each pattern contains one or more wildcard characters (*) which can match an arbitrary part of a sentence. For example, the pattern
I need *can match sentences like “I need ice cream” or “I need my father to love me”. - A list of replies. A reply can also contain a wildcard character, which will be replaced with the reflection of the match. For example, one of the responses for the
I need *pattern isWhy do you need *?, which produces answers like “Why do you need ice cream?” or “Why do you need your father to love you?”
Let’s start by defining a type for our rules.
struct Rule {
let pattern: String
let replies: [String]
func matchFor(sentence: String) -> String? {
return nil
}
}The match(sentence:) function will return the part of a sentence matched by wildcard in the pattern. The match between “I need ice cream” and the pattern I need * is “an ice cream”.
Obviously, a rule matches only a specific type of sentence. For example, the pattern above does not produce a match for the sentence “I think I am depressed”. That’s why the match(sentence:) returns an optional.
Imperative code is sometimes easier to write than functional code
We can put the list rules in our StaticData structure.
extension StaticData {
static var rules: [Rule] = [
Rule(pattern: "", replies: ["Speak up! I can't hear you."]),
Rule(pattern: "I need *", replies: [
"Why do you need *?",
"Would it really help you to get *?",
"Are you sure you need *?"])
]
}There are too many rules to report here. You can find the complete list in the Xcode project.
We can now write the whole Eliza algorithm, in which we:
- look for a rule that produces a match for the user’s message;
- pick a random reply;
- reflect the pronouns and the verbs in the match;
- replace the wildcard in the answer with the reflected match.
This description of the algorithm is not functional. That’s ok. We are still writing Swift. We can write the algorithm using a for loop.
private extension Eliza {
func transform(message: String) -> String {
for rule in StaticData.rules {
guard let match = rule.matchFor(sentence: message) else {
continue
}
let reply = Int.random(in: 0 ..< rule.replies.count)
return rule
.replies[reply]
.replacingOccurrences(of: "*", with: Reflector().reflect(sentence: match))
}
return "..."
}
}You can, of course, turn this code into functional code as well.
Doing so is not straightforward, though. Sometimes thinking in terms of loops is more natural than thinking about transforming sequences.
Here is how the transform(message:) would look like.
private extension Eliza {
func transform(message: String) -> String {
return StaticData.rules
.map { ($0, $0.matchFor(sentence: message)) }
.first(where: { (rule, result) in result != nil })
.map { (rule, result) -> String in
guard let result = result else { return "" }
return rule.replies[Int.random(in: 0 ..< rule.replies.count)]
.replacingOccurrences(of: "*", with: Reflector().reflect(sentence: result))
} ?? "..."
}
}As you can see, loops need to be transformed into the sequential application of map, filter and reduce (or derivative, convenience functions like first(where:) above). This is not as readable as a loop and can have a worse performance as well.
Beware that the last map(_:) is called on the Optional type and not on a sequence. I talk more in detail about that in my guide on Swift optionals.
Section 4:
Recursion

In functional programming you can write any program that you can write using imperative programming. This means that the functional paradigm needs a mechanism to replicate loops.
This mechanism is recursion, which is not only useful in functional programming, but also to handle complex data structure in your imperative programs.
The functional way of expressing loops: recursion
We finally got to the heart of functional programming.
How is it possible to write programs without loops?
The answer is recursion.
With recursion, we solve a problem by dividing it into smaller problems of the same type and then combining their results.
As usual, an example is easier to understand than a definition.
A typical example for recursion is calculating the factorial of a positive integer n, denoted by n!, which is the product of all the positive integers that come before n.
For example 5! = 5 ✕ 4 ✕ 3 ✕ 2 ✕ 1 = 120
This is an iterative description. Following it, we can write an imperative function that uses a loop.
But, if we look at the problem from the point of recursion, the factorial of an integer is that integer multiplied by the factorial of the previous one.
So, we can rewrite 5! as 5 ✕ 4!
In programming, a recursive function uses the result of calling itself on a subset of the problem.
func factorial(of number: Int) -> Int {
if number == 0 {
return 1
}
return number * factorial(of: number - 1)
}Notice an important detail. Any recursive function needs one or more base cases for which we have a predefined solution. A base case is necessary to stop the recursion. Otherwise, recursion will go on indefinitely.
In our factorial(of:) function, the base case is 0. This is not arbitrary. The mathematical definition of 0! is 1.
Recursion is a concept that was introduced, again, by lambda calculus but it’s not limited to functional programming.
Even in imperative programming, recursion is a more intuitive way to solve some problems. That’s true mainly when you use complex data structures like linked lists, trees and graphs.
You could solve these problems using loops, but that would be much harder than using recursion.
Iterating over sequences using recursion
Since recursion is the functional way of expressing loops, it’s essential to understand how that works on sequences.
We will start with a simple example. Let’s say we want to write a function that takes an array of numbers and doubles them.
Recursion consists of solving smaller parts of the same problem and combining the solutions.
What is the smallest problem we can think of in this case?
An empty array.
Starting from there, we can make the problem bigger, one step at a time.
- Doubling an empty array produces an empty array. This is our base case.
- Doubling an array of numbers means doubling the first element and appending to it the double of the rest of the array.
At some point, the recursion we will get to the end the array, where the remaining elements are the empty array. This is the base case that stops the recursion.
func double(of numbers: [Int]) -> [Int] {
if numbers.isEmpty {
return []
}
let first = numbers[0] * 2
return [first] + double(of: Array(numbers.dropFirst()))
}
double(of: [1, 2, 3, 4, 5])
// retunrs [2, 4, 6, 8, 10](To keep the example simple, I transformed the result of dropFirst(), which is an array slice, into an array.)
More in general, this is how you iterate recursively over sequences.
You apply your step to the first element and combine it with a recursive call on the remaining items. To stop the recursion, you need to provide a base case for the empty sequence.
As an example, we can now rewrite the map(_:) function without using a loop.
extension Array {
func recursiveMap<T>(transform: (Element) -> T) -> [T] {
if self.isEmpty {
return []
}
let first = transform(self[0])
return [first] + Array(self.dropFirst()).recursiveMap(transform: transform)
}
}
let numbers = [1, 2, 3, 4, 5]
numbers.recursiveMap { $0 * 3 }
// returns [3, 6, 9, 12, 15]Expressing the solution for a problem recursively
Now that you know the gist of recursion, we will implement the matching algorithm for Eliza. This is not a trivial problem, and it’s easier to solve it with recursion than with loops.
Before we proceed, a warning.
This function will be complicated.
Arguably, this is not the most straightforward example to learn recursion, but you can find plenty of those on the web.
It’s only with complex problems that you can understand the power of recursion. If you want to get familiar with the concept, you have to go past the simple examples and try to wrap your head around harder problems.
First of all, we need a recursive definition of finding the match between a pattern and a sentence. In general, a match between exists only when:
- you can fit a part of the sentence into the wildcard of the pattern, and
- the other letters in the sentence and the pattern match precisely.
From this, we can get an idea on what we will use recursion: the characters in each string.
Defining the base cases of a recursive algorithm
The matching algorithm is especially complicated because we have two on which we need to use recursion.
This also means that we will have many base cases and many recursive calls in our function, to cover all the possible combinations.
Let’s start defining the base cases.
We are using recursion on two strings, so we need a base case for when we reach the end of either one or both.
- If both strings are empty, they match. So, the match is the empty string.
- If one of the two string is empty, but the other isn’t, there is no match. In that case, we return
nil.
Rule {
let pattern: String
let replies: [String]
func matchFor(sentence: String) -> String? {
return match(between: pattern.lowercased(), and: sentence)
}
}
private extension Rule {
func match(between pattern: String, and sentence: String) -> String? {
switch (pattern, sentence) {
case ("", ""): return ""
case ("", _), (_, ""): return nil
default: return ""
}
}
}A couple of notes:
- The
matchFor(sentence:)method only takes one parameter, since it uses thepatternproperty of theRulestructure. Since we need to use recursion on two parameters, we need an extramatch(between:and:)method. - I am using a
switchstatement with pattern matching, which is another common feature of functional languages.
Solving a recursive problem using a tail call
Let’s now get to the recursive calls.
Our recursion operates on the first character of each string only. This gives us two combinations: the first character of the pattern is either a wildcard or not.
This is the easy part. Each case though has its sub-cases.
We will start from when the first character of the pattern is not a wildcard since it’s the easiest of the two.
- If the pattern character is different from the first character in the sentence, there is no match.
- Otherwise, we look for a match in the rest of both strings.
In general, when using recursion, you can find a solution to your problem in two ways:
- the solution is the result of a recursive call, or
- the solution is assembled from the result of a recursive call and some other value.
In this case, we are using the first of the two options, which is called tail call. Functional languages, including Swift, use a technique called tail call optimization to make recursion as efficient as loops in other languages.
It is sometimes possible to transform non-tail call recursion into tail call recursion. Beware though that while Swift performs tail call optimization, it does not guarantee it. So, if your code becomes too complex and you don’t have a performance problem, don’t bother.
Our code for this case is as follows:
private extension Rule {
func match(between pattern: String, and sentence: String) -> String? {
switch (pattern, sentence) {
case ("", ""): return ""
case ("", _), (_, ""): return nil
case (let pattern, let sentence) where pattern.first != "*":
return pattern.first == sentence.first
? match(between: pattern.droppingFirst(), and: sentence.droppingFirst())
: nil
default: return ""
}
}
}
extension String {
func droppingFirst() -> String {
return String(self.dropFirst())
}
}Here I used the ternary operator, which is more concise, but you can use a normal if statement if you prefer.
In functional languages, all statements return values, so there is no need for the return keyword. Using the ternary operator here looks “more functional”.
At the time of writing, there is a Swift evolution proposal in active review to make the return keyword optional in some cases.
Assembling the solution of a problem after a recursive call
Our second recursive case happens when the first character of the pattern is a wildcard.
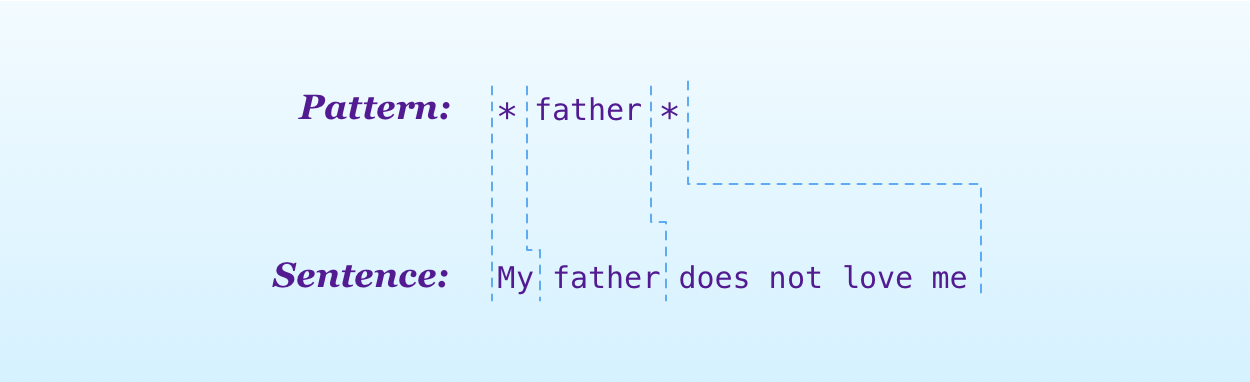
Not all patterns have a wildcard at the end. For example, there is a rule that detects any sentence where you mention the word mother.
extension StaticData {
static var rules: [Rule] = [
Rule(pattern: "", replies: ["Speak up! I can't hear you."]),
Rule(pattern: "I need *", replies: [
"Why do you need *?",
"Would it really help you to get *?",
"Are you sure you need *?"]),
Rule(pattern: "* mother *", replies: [
"Tell me more about your mother.",
"What was your relationship with your mother like?",
"How do you feel about your mother?",
"How does this relate to your feelings today?",
"Good family relations are important."])
]
}Unlike other rules, this one has more text after the wildcard. This means that in our matching algorithm when we find the wildcard, we have to look at the rest of the two strings to see if there is a match.
- If the rest of the two strings produce a match, the match is the first character of the sentence.
- Otherwise, the wildcard might match more letters. Here, the match is composed of the first character of the sentence and the match between the whole pattern and the rest of the sentence.
- If none of the two cases above is true, then there is no match.
This is the hardest part of the algorithm. The solution makes sense only when you consider all the cases at the same time.
When we find the wildcard character, we advance on the sentence until we get to the longest match that allows the end of the pattern and the sentence to match.
This is an example of a very complex problem that is more easily solvable with recursion. This is not tail recursion, and there is no way of making it so.
private extension Rule {
func match(between pattern: String, and sentence: String) -> String? {
switch (pattern, sentence) {
case ("", ""): return ""
case ("", _), (_, ""): return nil
case (let pattern, let sentence) where pattern.first != "*":
return pattern.first == sentence.first
? match(between: pattern.droppingFirst(), and: sentence.droppingFirst())
: nil
default:
if let _ = match(between: pattern.droppingFirst(), and: sentence.droppingFirst()) {
return String(sentence.first!)
} else if let longMatch = match(between: pattern, and: sentence.droppingFirst()) {
return String(sentence.first!) + longMatch
} else {
return nil
}
}
}
}It took me a while to wrap my head around this code.
I would not even know where to start writing this algorithm using a for loop. So, don’t worry if you don’t get it. I hope you still learned a ton from the rest of the article.
Our Eliza algorithm is finally complete.
Conclusions
As we have seen, functional programming has some desirable properties tied to readability, testing, and concurrency.
So, while Swift is not a functional language, you can get some benefits by writing parts of your code in a functional style.
Like anything, though, it can get out of hand.
- Some code is more readable in the imperative style. You can try and force the functional style on any piece of code you write, but in some cases, it is just unproductive.
- Keep also in mind that most Swift developers are familiar only with imperative code. New team members might have a hard time understanding your functional code, especially if you start using custom operators or a Swift functional programming library.
- Finally, recursion is not always the most performant way of writing code. Granted, often your data is so small that there is no perceivable difference. Nonetheless, the complexity of recursion is comparable to the one of loops only in the case tail recursion. Imperative solutions that use loops are more performant, so use recursion only when it makes solving a problem more manageable.
Personally, I write most of my code in imperative style, but I do write some functional code where it makes sense. More in general, I use concepts from functional programming in the architecture of my apps, to get the benefits I listed above.
One clear example is using value types for the model of an app, following the MVC pattern. Moreover, in SwiftUI, views are also value types, so the MVC pattern is even more crucial. You can find out why in my free guide below.
SwiftUI App Architecture: Design Patterns and Best Practices

It's easy to make an app by throwing some code together. But without best practices and robust architecture, you soon end up with unmanageable spaghetti code. In this guide I'll show you how to properly structure SwiftUI apps.
Matteo has been developing apps for iOS since 2008. He has been teaching iOS development best practices to hundreds of students since 2015 and he is the developer of Vulcan, a macOS app to generate SwiftUI code. Before that he was a freelance iOS developer for small and big clients, including TomTom, Squla, Siilo, and Layar. Matteo got a master’s degree in computer science and computational logic at the University of Turin. In his spare time he dances and teaches tango.


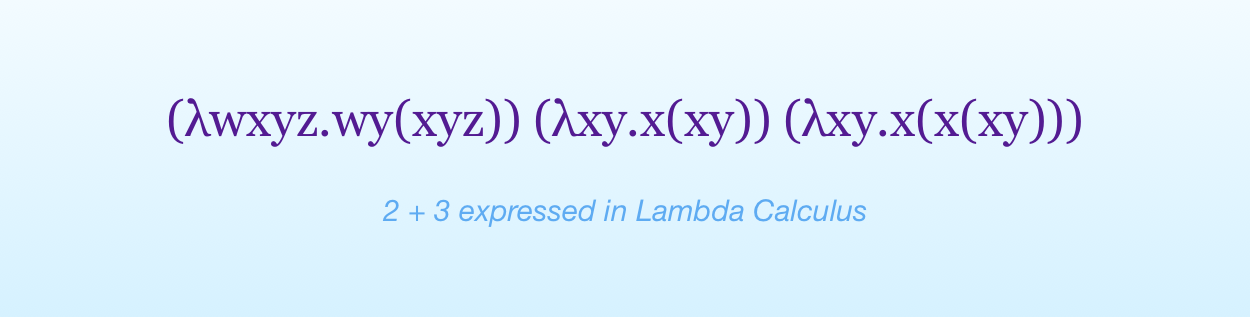
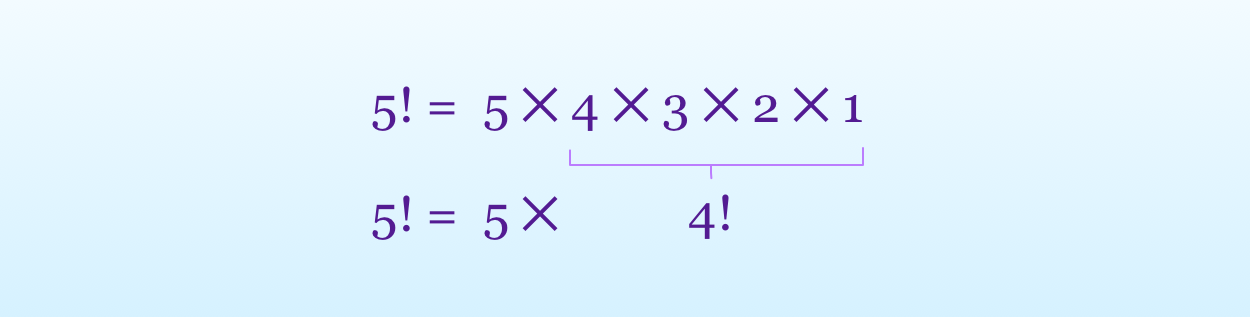

Very detailed review. I full heartedly agree with the conclusions. Swift has given us a lot of nice options that were impossible or hard to grasp compared to Objective-C. The syntactic sugar also helps a lot.